Pendulum Kinetics

Pendulum Kinetics#

A pendulum submerged in a fluid with the bob initially held at an angle of \(\theta^{\circ}\) degrees measured from below the horizontal, is released from rest as illustrated below.

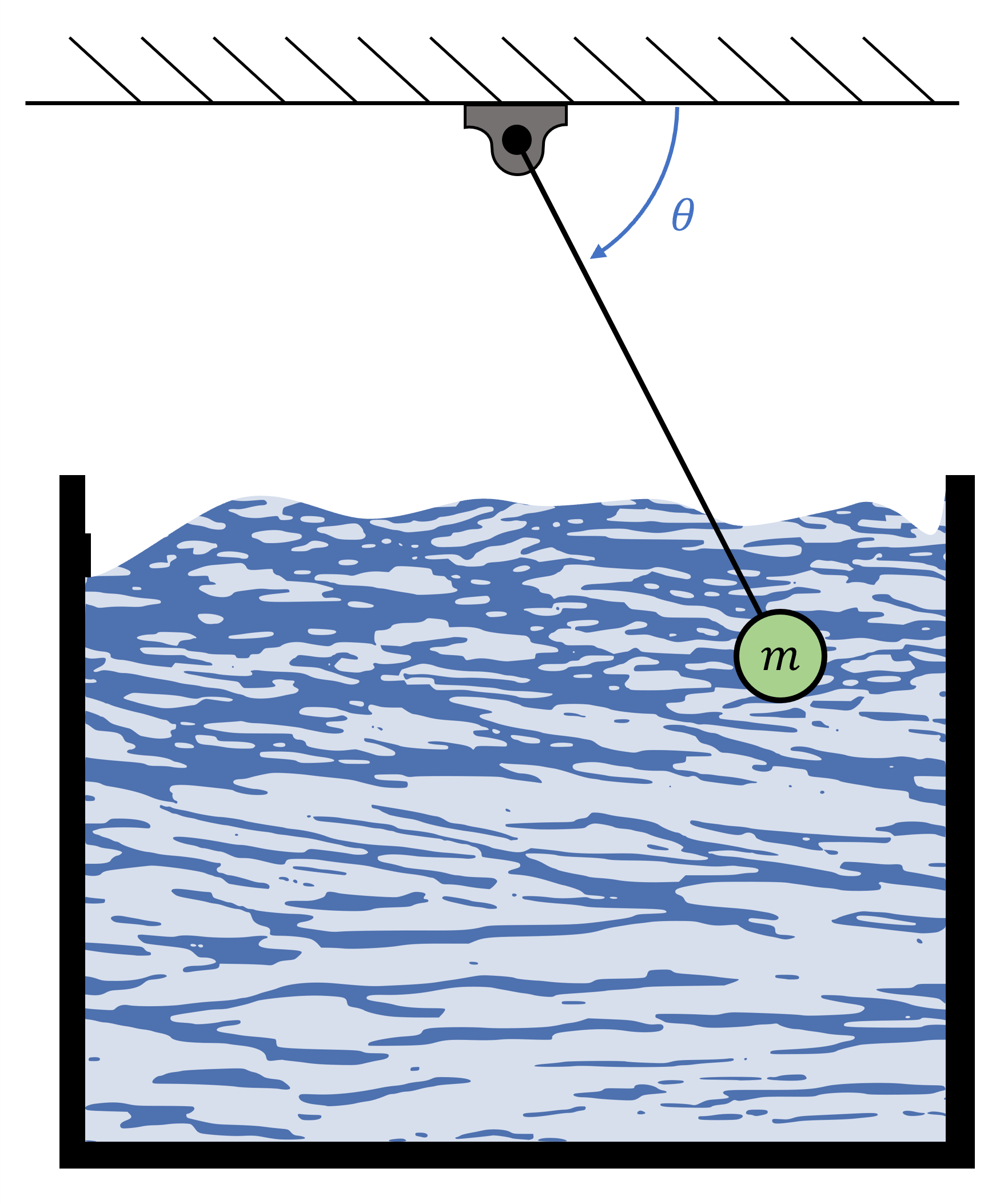
../../../../_images/part113.png

Part 1#

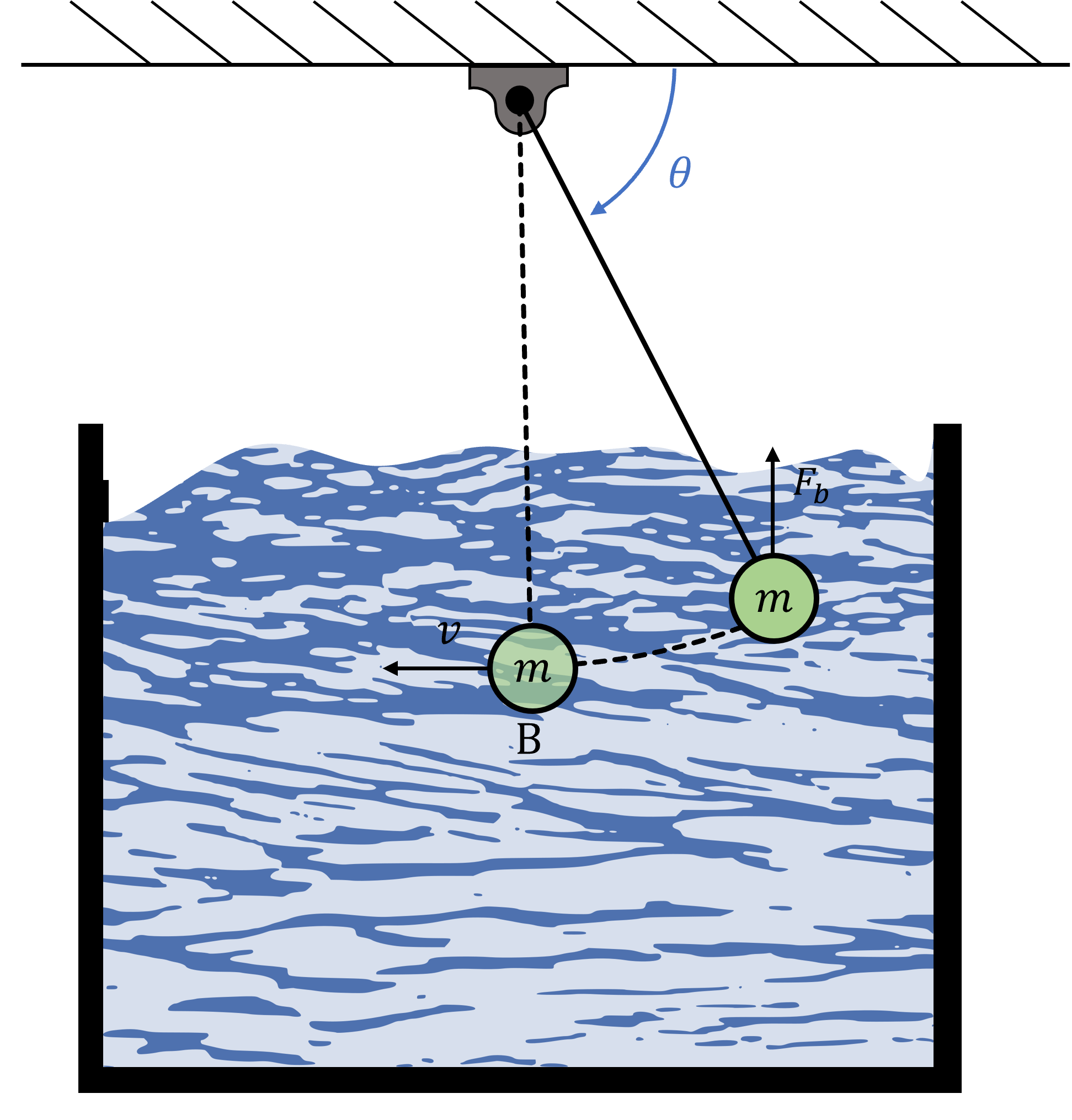
If in addition to the tension in the string and weight of the bob, a buoyant force of constant magnitude and direction acts on the bob according to the equation; \(F\_{b}=\rho g V\), where \(\rho\) is the fluid density, \(V\) is the volume of fluid displaced, and \(g\) is the gravitational acceleration. Determine the work-done by the buoyant force on the bob when it reaches point B as shown below.
\(\theta = {{ params.theta }}^{\circ}\), \(L = {{ params.l }} \ \rm{m}\), \(V\_{bob} = {{ params.v }} \ \rm{m^3}\), \(\rho = {{ params.p }}\ \rm{kg.m^{-3}}\).

../../../../_images/part25.png

Answer Section#

Please enter in a numeric value in \(\rm{N.m}\).

Part 2#

Determine the speed of the bob at point B.
\(m = {{ params.m }} \ \rm{kg}\).

Answer Section#

Please enter in a numeric value in \(m/s\).

Part 3#

Determine the maximum tension force in the string through the pendulum motion.

Answer Section#

Please enter in a numeric value in \(N\).

Part 4#

Determine the centripetal force in the string at point B.

Answer Section#

Please enter in a numeric value in \(N\).

Attribution#

Problem is licensed under the CC-BY-NC-SA 4.0 license.
The Creative Commons 4.0 license requiring attribution-BY, non-commercial-NC, and share-alike-SA license.